Вынужденные колебания - колебания, возникающие под действием периодически действующей силы. Для локомотива такой силой могут быть импульсы со стороны рельсового пути (например, от стыков), неровности пути.
Из теории колебаний угловая частота собственных колебаний надрессорного строения тележки при вертикальных колебаниях (подпрыгивании) определяется по формуле
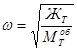, с-1 (17)
Здесь: Жт - жесткость тележки, определяемая по формуле (16), но в размерности Н/м;
- обрессоренная масса, действующая на одну тележку.
Ориентировочно
= 0,1 ∙ 
∙ 103, кг.
Тогда линейная частота будет равна.
, (17’)
Во время работы тепловоза в процессе колебаний возникают динамические нагрузки на рессорное подвешивание и далее на колесные пары, которые оцениваются коэффициентом динамики Кд:
(18)
Статический прогиб в этой формуле fст - в мм.
Грузовые тепловозы имеют Vконст = 100 км/ч.
Определив коэффициент динамики, можно найти динамические нагрузки
(19)
Величина Рдин, полученная по формуле (19), не должна превышать Рст более чем на 30-40 %.
При вынужденных вертикальных колебаниях, возникающих от периодического воздействия стыков рельсового пути, может наступить резонанс (когда частота собственных колебаний совпадает с частотой вынужденных колебаний системы). Критическая скорость локомотива, при которой наступает это явление, определяется по формуле
Vкрит=3,6L ∙ υ, км/ч,
где L - длина рельса, м.
Локомотивы проектируются так, чтобы Vкрит ≥ Vконст .
В нашем случае индивидуальное рессорное подвешивание и:
=0,1 ∙ 790,5 ∙ 103 = 79,05 ∙ 103 кг
кН/мм = 1129,3 ∙ 104 Н/мм
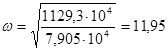с-1
Гц
При длине рельса L = 12,5 м
Vкрит=3,6 ∙ 12,5 ∙ 1,9 = 85,5 км/ч,
При длине рельса L = 25 м
Vкрит=3,6 ∙ 25 ∙ 1,9 = 171 км/ч.
Таким образом, наш локомотив с данной жесткостью рессорного подвешивания не может двигаться с конструктивной скоростью 160 км/ч по рельсовой колее с длиной рельса 12,5 м